Преобразования в трех мерной системе координат
В трех мерной системе координат используются следующие базовые преобразования:
Перенос точки на заданный вектор;
Поворот на заданный угол относительно координатной оси;
Перенос системы координат на заданный вектор;
Поворот системы координат на заданный угол относительно координатной оси;
Зеркальное отображение точки относительно координатной плоскости XY ;
Зеркальное отображение точки относительно плоскости XY ;
Зеркальное отображение точки относительно координатной оси XZ ;
Смена направление координатной оси;
Изменение масштаба координат по оси X ;
Изменение масштаба координат по оси Y .
Изменение масштаба координат по оси Z .
Перенос точки на вектор U , задаваемый параметрами u x , u y , u z , предполагает следующее преобразование координат:
x a’ = x a - u x ;
y a’ = y a – u y ;
z a ’ = z a – u z .
Используя однородную систему координат, данные преобразования в матричной форме можно представить в виде:

a ,b ,c – параметры вектора переноса.
Легко показать, что матрица обратного преобразования (или матрица переноса системы координат) в этом случае будет иметь вид:

Поворот относительно координатной оси.
Поворот относительно оси Z .
Данный вид преобразования иллюстрируется ниже приведенным рисунком (Рис. 5.2‑1), где приводится поворот точки А на угол a .
 |
Рис. 5.2 ‑ 1
Из приведенного рисунка видно, что поворот относительно оси Z не меняет координаты точки по координатной оси Z . Что же касается изменений координат по оси X и Y , то они аналогичны изменениям по осям X ,Y в двумерной координатной системе, так как новая и старая точки остаются в одной плоскости, параллельной координатной плоскости X ,Y . Таким образом, использую уравнения (5.1-5) и (5.1-6), будем иметь:
x b ’ = x b cos a - y b sin a + 0;
y b’ = x b sin a + y b cos a +0;
z b ’ = 0 +0 +z .
Данные преобразования можно представить в матричной форме как:
 (5.1-7)
(5.1-7)
Поворот относительно оси X .
Координатные оси в трехмерной системе равнозначны, поэтому поворот относительно координатной оси X , аналогично повороту относительно оси Z , можно представить как:
y b’ = y b cos a - z b sin a + 0;
z b’ = y b sin a + z b cos a +0;
x b ’ = 0 +0 +x .

Для того, чтобы координаты матриц перечислялись в том же порядке, что и в выражении (5.1-7), необходимо их циклически сдвинуть в сторону элемента с большим индексом, т.е. вправо. При этом соответствующий сдвиг необходимо выполнить и в матрице начальных координат. Что же касается двумерной матрице, то ее колонки необходимо циклически сдвинуть вправо (в сторону колонки с большим индексом), а затем циклически сдвинуть строки вниз (в сторону строки с большим индексом), как это показано ниже.
 (5.1-8)
(5.1-8)
Поворот относительно оси Y .
Координатные оси в трехмерной системе равнозначны, поэтому поворот относительно координатной оси Y , аналогично повороту относительно оси Z , можно представить как:
z b ’ = z b cos a - x b sin a + 0;
x b ’ = z b sin a + x b cos a +0;
y b ’ = 0 +0 +y .
Соответственно в матричной форме будем иметь:

Для того, чтобы координаты в матрице перечислялись в том же порядке, что и в выражении (5.1-7), необходимо их циклически сдвинуть в сторону элемента с меньшим индексом, т.е. влево. При этом соответствующий сдвиг необходимо выполнить и в матрице начальных координат. Что же касается двумерной матрице, то ее колонки необходимо циклически сдвинуть влево (в сторону колонки с меньшим индексом), а затем циклически сдвинуть строки вверх (в сторону строки с меньшим индексом), как это показано ниже.
 (5.1-8),
(5.1-8),
Таким образом, матрицы базового поворота на угол a по отношения к координатной оси будут иметь вид:


 (5.1-9),
(5.1-9),
Легко показать, что матрицы соответствующих обратных преобразований (или матрицы поворота системы координат относительно координатных осей), будут иметь вид:


 (5.1-10)
(5.1-10)
Зеркальное отображение точки относительно координатной плоскости XY .
зависимости координат.
Для отображения относительно координатной плоскости XY :
x a’ = x a
Y a’ = y a ;
Z a’ = -z a .

Для отображения относительно координатной плоскости XZ ;
x a’ = x a
Y a’ = - y a ;
Z a’ = z a
В матричной форме это преобразование записывается как:

Для отображения относительно координатной плоскости ZY :
x a’ = -x a
Y a’ = y a ;
Z a’ = z a .
Матричная запись будет иметь вид:

Смена направления координатной осей
Преобразование координат при смене направленности координатных осей X ,Y ,Z отображается, соответственно, следующими матрицами.



Изменение масштаба по координатным осям .
Преобразования этого типа предполагает следующие зависимости координат:
x a’ = r x a ;
Y a’ = l y a ;
Z a ’ = f z a ,
где r , l , f – вводимые масштабные коэффициенты по соответствующим координатным осям.
В матричной форме это преобразование записывается как:

Рассмотрим сложное преобразование координат в трехмерной системе.
Предположим необходимо выполнить поворот точки относительно произвольного вектора в трех мерной системе координат, как это показано на Рис. 5.2‑2.
Сначала решим рассматриваемую задачу для частного случая. Предположим, что вектор U , относительно которого нужно повернуть точку А на угол a , проходит через начало системы координат (Рис. 5.2‑3).
Вектор, относительно которого необходимо выполнить поворот, можно задать в сферических координатах, т.е. через тройку параметров: q, j, r, где:
R - модуль вектора U ;
J - угол между вектором U и координатной осью Z ;
Q - угол между проекцией r ’ вектора U на координатную плоскость XY и координатной осью X .

Рис. 5.2 ‑ 2
При таком частном случае заданное преобразование поворота точки относительно заданного вектора можно выполнить за счет последовательности следующих базовых преобразований:
1)поворот исходной системы координат относительно координатной оси Z на угол q ;
2)поворот новой системы координат относительно оси Y на угол-j ;
3)поворот точки А относительно координатной оси Z ’’на угол a ;
4)поворот системы координат на угол j относительно оси Y ;
5) поворот системы координат относительно координатной оси Z на угол-q .
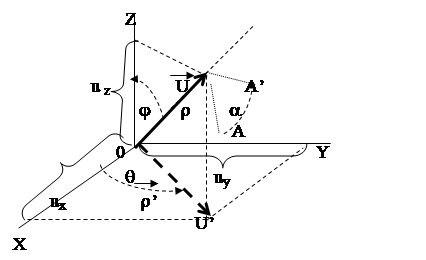 |
Рис. 5.2 ‑ 3
1-ый поворот исходной системы координат относительно ее оси Z на угол q формирует новую систему координат X ’Y ’Z ’, в которой ось X ’ совпадет с r ’, ось Y ’ будет повернута по отношению к оси Y на угол q , ось Z ’ совпадает с осью Z , что показано на Рис. 5.2‑4.
 |
Рис. 5.2 ‑ 4
Отметим, что в новой системе координат вектор U лежит в координатной плоскости X ,Z .
Поворот осуществляется при использовании матрицы обратного преобразования типа «поворот относительно координатной оси Z ».
2-ой поворот формирует систему координат X ”Y ”Z ”, в которой ось X ” повернута относительно оси X ’ на угол (-j ) (угол поворота отрицательный, так как для совмещения оси Z новой системы координат с вектором U поворот нужно выполнить в направлении по часовой стрелке), ось Y ’’ совпадает с осью Y ’, ось Z ” совпадает с вектором U .
Рассматриваемому повороту соответствует матрица базового поворота точки относительно оси Y .
3-ий поворот. В системе координат, полученной после выполнения двух предыдущих поворота, заданный вектор U совпадает с осью Z ”, что позволяет выполнить в этой системе заданный поворот за счет базового поворота относительно оси Z ”.
4-ый поворот обеспечивает возврат к системе координат X ’,Y ’,Z ’ и реализуется с помощью матрица обратного преобразования типа «поворот относительно координатной оси Y » на угол j .
5-ый поворот обеспечивает возврат к начальной системе координат X ,Y ,Z и реализуется с помощью матрица преобразования типа «поворот относительно координатной оси Z » на угол -q .
Таким образом, формирование координат точки при рассматриваемом сложном преобразовании осуществляется через произведение матриц элементарных преобразований следующего вида:
 (5.1-10)
(5.1-10)
X и , y и , z и – исходные кордиинаты точки;
X пч , y пч , z пч – новые кордиинаты после поворота для рассматриваемого частного случая;
-

-

-

-

-
При решении рассматриваемой задачи для общего положения в пространстве вектора U , используется те же действия, что и в рассмотренном частный случай, с добавлением в начале преобразований перенос исходной системы координат в точку D (см Рис. 1.2‑1) и в конце - перенос начало координат из точки D в точку начала координат исходной системы.
Таким образом, для общего положения вектора поворота, новые координаты точки А после заданного поворота определяются через произведение матриц элементарных базовых преобразований следующим образом:
(5.1-11)
x п, y п, z п - координаты положения точки после поворота;


Переход от одной формы задания вектора к другой.
Вектор, который часто используется в процессе преобразований координат, иногда удобно задавать в полярных координатах (например, при поворотах), а иногда в декартовых координатах (например, при переносах). На практике вектор задается только одним из этих способов. Для перехода от одной формы задания вектора к другой используются следующие соотношения.
Переход от декартового к полярному представлению вектора
При задании вектора U в полярных координатах в виде тройки {r,j,q}, как следует из Рис. 5.2‑3, имеет место:
u z =r cos j ;
u x =r sin j cos q ;
u y =r sin j sin q ;
Переход от полярного к декартовому представлению вектора
При задании вектора U в декартовых координатах в виде тройки {u x , u y , u z }, как следует из Рис. 5.2‑3, имеет место:
![]()
j = arc cos (u z ./ r );

В выражении (5.1-11) в качестве сомножителей выступают матрицы разных размерностей (3*3 и 4*4). Для того, чтобы найти их произведение, необходимо привести матрицы к одной размерности, т.е. матрицы размерности 3*3 необходимо расширить до размерности 4*4. Однако с расширением размерности не надо спешить. Пользуясь свойством ассоциативности произведения матриц, умножение матриц следует выполнять в последовательности, определенной скобками в ниже приведенной версии выражения (5.1-11):
(5.1-12)
Обозначение матрицы знаком «*» означает использование расширенной матрицы.
Такой прием позволяет уменьшить затраты времени на выполнение умножений матриц.
В выражении (5.1-11) произведение первых трех матриц обеспечивает переход от исходной системы координат к системе координат, «удобной» для заданного преобразования. Что касается произведения последних трех матриц, то они обеспечивают переход от «удобной» системы координат к исходной. По этому, используя свойство ассоциативности, выражение (5.1-11) можно представить как:
(5.1-13)
R 1 – матрица перехода от исходной к «удобной» системе координат;
R 1 -1 –матрица, обратная матрице R 1.
В некоторых случаях, с точки зрения затрат времени, реализация выражения (5.1-12), может быть предпочтительнее, чем реализация выражения (5.1-11). В свою очередь, может оказаться удобнее формировать матрицу R 1 -1 не через произведение трех матриц (см. выражение(5.1-13), а получить ее, рассчитав ее элементы как элементы матрицы, обратной матрице R 1.
Матрица, обратная заданной, может быть найдена следующим образом.
Из определения обратной матрицы следует, что матрица В является обратной по отношению к заданной матрице А, если имеет место равенства:
А*B =E ,
где Е – единичная матрица, имеющая вид:

Отсюда элементы обратной матрицы могут быть найдены из системы уравнений.
Часть 8 - интегрирование угловых скоростей, матрицы поворота
Часть 11 - интегрирование угловых скоростей, методы высших порядков (в разработке)
Интегрирование угловых скоростей с помощью матриц поворота
Продолжаем нашу предвыборную гонку - какой интегратор угловых скоростей займёт своё законное место у руля (в буквальном смысле) нашего изделия?
Мы уже накопали компромата на углы Эйлера-Крылова - это конечно уважаемые и достойные фамилии, но очень уж старенькие - задрать голову в зенит не могут, сразу начинает голова кружиться, да и подвешенные вниз головой резко теряют работоспособность. Да и вообще, уголовники (системы, основанные на углах) нам не нужны!
Сегодня мы рассмотрим матрицы поворота - 9 направляющих косинусов не могут ошибаться, не правда ли?
Кинематическое уравнение для связанных осей (когда угловая скорость проецируется на оси изделия) принимает вид:
Здесь A – матрица ориентации.
Для шага Δt мы можем записать приближенный метод интегрирования:
Этот метод – сугубо линейный, в нём применяются только сложения и умножения, особые точки отсутствуют как класс.
Один недостаток, который мы можем заметить «сходу» - это громоздкость: мы используем 9 чисел для представления матриц, а каждый шаг интегрирования по простейшему методу («первого порядка») требует 18 умножений и 18 сложений (без специализированного метода, «знающего» о единицах по главной диагонали – и вовсе 27 умножений). Если выписать по компонентам, мы получим (с верхним индексом 1 – новые значения, с верхним индексом 0 – старые):

Матричная запись позволяет скрыть эту внутреннюю сложность за красивыми выкладками, поэтому полезно иногда выписать вычисления «в лоб», чтобы помнить, с чем мы имеем дело.
Тем не менее, даже у самых старых бортовых вычислителей не возникло бы проблем, связанных с недостаточной производительностью – ну что такое 36 операций для компьютера!?
Нет, настоящая ахиллесова пята матриц поворота состоит в том, что по прошествии времени они перестают быть матрицами поворота, а вернуть их на путь истинный не так-то просто…
Пусть начальная матрица ориентации – единичная, то есть оси инерциальной и связанной систем координат совпадают:


После 72 шагов придём к матрице ориентации, равной:
тогда как должны были прийти к единичной матрице (поворот на 360 градусов!).
Можем записать эту матрицу, как произведение двух:
Вторая из них – матрица поворота по оси Z на угол 0,9° - такова накопленная ошибка интегрирования, вызванная слишком крупным шагом. В относительном выражении ошибка не так велика: 0,9/360 = 0,25%, что не так уж плохо, учитывая, сколь крупный шаг мы взяли.
А вот первая матрица – масштабирование по осям X, Y. Вектор с нулевой компонентой Z просто увеличит свою длину – зачастую это не так уж страшно – по крайней мере, это не изменит направление вектора. Точно так же, вектор (0;0;1) T останется без изменений – всё верно.
Самое интересное будет происходить с промежуточными векторами.
К примеру, вектор![]()
превратится в
он не только увеличивается в размерах, но и меняет направление из-за масштабирования! Раньше он «смотрел» под углом 45° к плоскости X-Y, а теперь – под углом 37° - ошибка составляет уже не 0,9°, а целых 8°!
В данном конкретном случае мы легко смогли факторизовать матрицу, вычленив из неё отдельно поворот и отдельно масштабирование. Когда мы можем это сделать – понятно, как исправить ситуацию – нужно оставить только матрицу поворота, а масштабирование убрать!
Но представим теперь, что после поворотов вокруг оси Z, мы осуществили ещё и поворот вокруг приборной оси X на 30 градусов:

Как из этого нагромождения чисел наиболее оптимально вычленить отдельно повороты, избавившись от других преобразований пространства – вопрос по-прежнему открытый…
Напомним, что столбцы матрицы ориентации – это координаты базисных векторов в инерциальной системе отсчета. Эти векторы должны иметь единичную длину и быть взаимно-перпендикулярными, то есть мы можем записать следующие «уравнения связи» (в данном случае двойка наверху – это возведение в степень):

Действительно: при 9 коэффициентах матрицы, мы должны иметь ровно 3 степени свободы, поэтому нам и нужны дополнительные 6 уравнений. Проверим, что происходит у нас:
Длина 1-го базисного вектора: 1,314
Длина 2-го базисного вектора: 1,243
Длина 3-го базисного вектора: 1,087
Угол между 1 и 2: 90°
Угол между 2 и 3: 103,47°
Угол между 1 и 3: 90°
Ортонормированный базис перестал быть таковым! Мы понимаем это, но как именно скорректировать 9 значений, чтобы он снова стал ортонормированным?
Можно применить старый добрый метод построения ортонормированного базиса. Исходные базисные векторы обозначим e 1 , e 2 , e 3 :
![]()
Преобразованный базис назовём n 1
, n 2
, n 3
.
Первый вектор мы нормируем:
![]()
Из второго вектора мы вычитаем его проекцию на первый, после чего тоже нормируем:
Наконец, из третьего вектора вычитаем его проекцию на первый и второй, после чего нормируем:

В этих формулах есть определённое лукавство: кажется, что мы задействовали все 9 исходных коэффициентов, чтобы получить новые 9, теперь уже ортонормированные. На самом деле, от e 3 вообще ничего не зависит! Сначала мы вычитаем из него всё лишнее, так, чтобы он шел по прямой, взаимно перпендикулярной n 1 , n 2 , а затем нормируем его длину – да от этого вектора живого места не остаётся! Мы с тем же успехом можем записать:
![]()
и получить абсолютно тот же самый результат! То есть, в действительности данный метод берёт первые 6 коэффициентов и напрочь выкидывает последние 3. Да и первые 6 оказываются неравнозначны: если первому столбцу мы доверяем «безоговорочно», то второму – только до тех пор, пока он не противоречит первому.
Попробуем процедуру нормировки на нашей матрице B:
При этом, как и следовало ожидать, n 3 получился одинаковым до последнего представимого знака после запятой, независимо от способа вычисления – через e 3 или через векторное произведение.
Сейчас нам повезло – мы идеально отнормировали матрицу, так что она выражает ровно то, что и должна – поворот на 0,9° вокруг оси Z и поворот на 30° вокруг оси X.
Но попробуем теперь зайти с обратной стороны – не e 1
, e 2
, e 3
, а e 3
, e 2
, e 1
. Получится вот что:

Вместо поворота на 30° по оси X, мы в этот раз получили поворот на 37°, реализовав фактически наихудший случай!
Правильным подходом было бы решение оптимизационной задачи: каждый коэффициент матрицы является суммой полезного сигнала и шума. Найти новые коэффициенты, выраженные через старые, таким образом, чтобы среднеквадратичная ошибка стремилась к минимуму. Но даже тогда мы не гарантируем наилучшей работы – кто сказал, что, используя приближенные матрицы конечного поворота, мы вносим именно случайную ошибку!?
Уточним, в чём наша проблема. Нам не хотелось выписывать точную матрицу конечного поворота, поскольку она выглядит примерно так:
(меняя порядок поворотов, будем получать разные матрицы W, но все они будут являться строго матрицами поворота)
Мы «из жадности» её упростили:

И обнаружили, что выкинутые нами слагаемые второго порядка малости приводят к изменению вида матрицы. В нашем примере поворота вокруг оси Z, получаем

Разложив в ряд Тейлора до 3-го порядка малости, имеем:

И снова мы наблюдаем похожий эффект: ошибка интегрирования на этот раз чрезвычайно мала, составляя менее угловой секунды, тогда как наиболее заметное искажение снова проявилось в масштабе. Кажется, что ошибка весьма мала – менее одной тысячной – но этого достаточно, чтобы вектор, направленный под углом 45° к плоскости XY, «прижался бы» к ней дополнительно на 1 угловую минуту.
Так что даже использование малого шага интегрирования и применение методов высокого порядка не решает проблему накопления «мусора» в матрице. И чем больше проходит времени, тем больше в матрице будет мусора, который мы сможем отбросить только вместе с полезными данными.
Всё сказанное не означает, что матрицы поворота абсолютно не годятся для интегрирования угловых скоростей. Их можно применить, если соблюдать определённую осторожность - обязательно предусмотреть процедуру "ортонормирования", но по возможности до неё не доводить - повсюду перейти на удвоенную или расширенную точность, уменьшить шаг интегрирования, использовать численные методы высокого порядка.
Но как мы узнаем в следующей главе, кватернионы свободны от большинства недостатков матриц поворота и выходят в этой битве победителями.
Продолжение следует...
Рассмотрим задачу о нахождении направляющих косинусах, задающих ориентацию подвижной системы координат Oxyz относительно некоторой, назовем ее неподвижной, системой координат OXYZ. Исходную систему координат подвижного трехгранника обозначим Ox 0 y 0 z 0 и до поворота она соответственно совпадала с системой координат OXYZ. Пусть трехгранник Oxyz переместился из положения Ox 0 y 0 z 0 в текущее в результате одного поворота на угол около оси On, заданной единичным ортом в системе координат OXYZ. Ось On может занимать разное направление, не обязательно совпадающим с одной из осей трехгранника OXYZ. Представим используемые системы координат и их связи граф-схемой:

 - матрица направляющих косинусов, задающая ориентацию трехгранника Ox v y v z v , одна из осей которого (пусть первая ось Ox v) задает ориентацию оси поворота On;
- матрица направляющих косинусов, задающая ориентацию трехгранника Ox v y v z v , одна из осей которого (пусть первая ось Ox v) задает ориентацию оси поворота On;
 - матрица поворота относительно оси On .
- матрица поворота относительно оси On .
Тогда искомая матрица конечного поворота определяется соотношением
![]() .
.
Или раскрывая выражение и используя свойства (1.9) , получим матрицу конечного поворота в следующем виде


 (1.11)
(1.11)

Направляющие косинусы, задающие ориентацию оси On поворота ПО на угол . Таким образом, положение подвижной системы координат задается с помощью четырех параметров: , .
Матричная форма формулы Эйлера
Пусть в системе координат СК m задана точка M, которая определена вектором
где – проекции вектора на оси системы координат СК m , что отмечено нижним индексом “m”.
Определим линейную скорость точки М в проекциях на оси системы координат СК m . Согласно формуле Эйлера имеем
![]() . (1.12)
. (1.12)
Здесь – вектор угловой скорости системы координат СК m относительно системы координат СК s , выраженный в проекциях этого вектора на оси системы координат СК m .
Используя матричную форму векторного произведения, запишем

Запишем полученный результат в матричной форме
![]() , (1.13)
, (1.13)
Где  (1.14)
(1.14)
Индекс “~ ” (тильда) указывает на кососимметричную форму данной матрицы.
Формула Пуассона
В традиционной форме обозначения угловую скорость можно представить в виде
Заметим, что в формуле (1.13) неявно было положено условие
В общем случае, когда выведем рабочее соотношение другим способом.
![]() Продифференцируем соотношение
Продифференцируем соотношение
Или в другой форме
![]() (1.18)
(1.18)
В двумерном пространстве поворот можно описать одним углом θ со следующей матрицей линейного преобразования в декартовой системе координат:
Положительным углам при этом соответствует вращение вектора против часовой стрелки в обычной, правосторонней системе координат, и по часовой в левосторонней системе координат.
Сам поворот происходит путём умножения матрицы поворота на вектор
Матрица поворота в трёхмерном пространстве
Матрицами вращения вокруг оси декартовой правой системы координат на угол α в трёхмерном пространстве являются:
Вращение вокруг оси x:
 ,
,
Вращение вокруг оси y:
 ,
,
Вращение вокруг оси z:
 ,
,
В трёхмерном пространстве для описания поворота можно использовать
Матрицы поворота вектора в декартовой системе координат, соответствующие первым двум способам задания поворота:
Однако, поскольку умножение матриц не коммутативно, то есть: , следовательно, положение системы координат после поворота вокруг трех осей будет зависеть от последовательности поворотов, то существует 6 различных видов матрицы поворота:
1) Поворот около осей: X -> Y -> Z
2) Соответственно: X -> Z -> Y
3) Y -> X -> Z
4) Y -> Z -> X
5) Z -> X -> Y
6) Z -> Y -> X
Получить же нужную матрицу можно путем последовательного перемножения матриц поворота около одной оси (приведенных выше) в соответствии с желаемым порядком.
Билет 33. Свойства обратной матрицы
33) Обра́тная ма́трица - такая матрица A −1 , при умножении на которую исходная матрица A даёт в результате единичную матрицу E :
1)![]() ,
где
обозначает
определитель.
,
где
обозначает
определитель.
2)для любых двух обратимых матриц A и B .
3)где * T обозначает транспонированную матрицу.
4)для любого коэффициента .
5)Если необходимо решить систему линейных уравнений Ax = b , (b - ненулевой вектор) где x - искомый вектор, и если A − 1 существует, то x = A − 1 b . В противном случае либо размерность пространства решений больше нуля, либо их нет вовсе.
Матричный метод решения (метод решения через обратную матрицу) систем линейных алгебраических уравнений с ненулевым определителем состоит в следующем.
Пусть дана система линейных уравнений с n неизвестными (над произвольным полем):

Тогда её можно переписать в матричной форме:
AX = B , где A - основная матрица системы, B и X - столбцы свободных членов и решений системы соответственно:

Умножим это матричное уравнение слева на A − 1 - матрицу, обратную к матрице A :
Так как A − 1 A = E , получаем X = A − 1 B . Правая часть этого уравнения даст столбец решений исходной системы. Условием применимости данного метода (как и вообще существования решения неоднородной системы линейных уравнений с числом уравнений, равным числу неизвестных) является невырожденность матрицы A. Необходимым и достаточным условием этого является неравенство нулю определителя матрицы A:
Для однородной системы линейных уравнений, то есть когда вектор B = 0, действительно обратное правило: система AX = 0 имеет нетривиальное (то есть ненулевое) решение только если det A = 0. Такая связь между решениями однородных и неоднородных систем линейных уравнений носит название альтернативы Фредгольма.
Билет 34. Теорема о связи решений однородной и неоднородной СЛАУ.
Неоднородная система: Ax=B, B≠0.
Однородная система: Ах=0.
Теорема: 1. Если вычесть два решения неоднородной системы, то получится решение однородной системы.
2. Если к решению неоднородной системы прибавить решение однородной системы, то получится решение неоднородной системы.
Доказательство:
1) с 1 ,с 2 – два решения неоднородной системы.
Ас 1 =В; Ас 2 =В. Из первой системы вычтем вторую систему: Ас 1 -Ас 2 =0; А(с 1 -с 2)=0; с 1 -с 2 – решение однородной системы.
2) Ас н =В – решение неоднородной системы.
Ас о =0 - решение однородной системы.
Ас н + Ас о =В. А(с н + с о)=В. с н + с о – решение неоднородной системы.
Билет 35. Несовместность СЛАУ. Метод Гауса.
Если система решений не имеет, то она называется несовместной.
Алгоритм решения СЛАУ методом Гаусса подразделяется на два этапа:
1)На первом этапе осуществляется так называемый прямой ход, когда путём элементарных преобразований над строками систему приводят к ступенчатой или треугольной форме, либо устанавливают, что система несовместна. А именно, среди элементов первого столбца матрицы выбирают ненулевой, перемещают его на крайнее верхнее положение перестановкой строк и вычитают получившуюся после перестановки первую строку из остальных строк, домножив её на величину, равную отношению первого элемента каждой из этих строк к первому элементу первой строки, обнуляя тем самым столбец под ним. После того, как указанные преобразования были совершены, первую строку и первый столбец мысленно вычёркивают и продолжают пока не останется матрица нулевого размера. Если на какой-то из итераций среди элементов первого столбца не нашёлся ненулевой, то переходят к следующему столбцу и проделывают аналогичную операцию.
2)На втором этапе осуществляется так называемый обратный ход, суть которого заключается в том, чтобы выразить все получившиеся базисные переменные через небазисные и построить фундаментальную систему решений, либо, если все переменные являются базисными, то выразить в численном виде единственное решение системы линейных уравнений. Эта процедура начинается с последнего уравнения, из которого выражают соответствующую базисную переменную (а она там всего одна) и подставляют в предыдущие уравнения, и так далее, поднимаясь по «ступенькам» наверх. Каждой строчке соответствует ровно одна базисная переменная, поэтому на каждом шаге, кроме последнего (самого верхнего), ситуация в точности повторяет случай последней строки.
Уравнение y=kx+b называется уравнением прямой с угловым коэффициентом; k - угловой коэффициент, b - величина отрезка, который отсекает прямая на оси Оу, считая от начала координат. Тангенс угла наклона прямой к оси Ох называется угловым коэффициентом прямой. k=tg(альфа).
Угол между двумя прямыми:
Первая прямая: L 1 , n 1 (p 1 ,q 1 ,r 1).
Вторая прямая: L 0 , n 0 (p,q,r).
L 1 // L 0 ; n 1 // n 0 ; p 1 /р=q 1 /q= r 1 /r – условие параллельности 2 прямых.
L 1 ﬩ L 0 ; n 1 ﬩n 0 ; (n 1 ,n)=0; pp 1 +qq 1 +rr 1 =0 – условие параллельности 2 прямых.
Cosφ=(n 1 ,n)/|n 1 |*|n 0 |
В плоскости Лобачевского две прямые могут либо пересекаться, либо могут быть параллельными в некотором направлении, либо расходящимися. Поэтому в плоскости Лобачевского существует три вида пучков прямых:
1) пучок прямых, пересекающихся в одной точке, называемой центром пучка; такой пучок называется центральным или эллиптическим;
2) пучок прямых, параллельных в заданном направлении некоторой прямой, называемой осью пучка; такой пучок называется параболическим;
3) пучок расходящихся прямых, перпендикулярных к некоторой прямой, называемой базой пучка; такой пучок называется гиперболическим.
Взаимное расположение прямых на плоскости.
Прямые линии в пространстве могут быть параллельными, пересекающимися и скрещивающимися. Рассмотрим подробнее каждый случай.
1. Параллельные прямые линии.
Параллельными называются две прямые, которые лежат в одной плоскости и не имеют общих точек.
Проекции параллельных прямых на любую плоскость (не перпендикулярную данным прямым) - параллельны. Если AB//CD то A 1 B 1 //C 1 D 1 ; A 2 B 2 //C 2 D 2 ; A 3 B 3 //C 3 D 3 (рис.33). В общем случае справедливо и обратное утверждение.
Матрица поворот применяется для вращения системы координат или объекта, сцены.
Матрицы поворота вокруг основных осей.
Матрица поворота вокруг произвольной оси.
Обобщённая матрица поворота.
Хочется задавать положение объекта в пространстве однозначно. Достаточно очевидно что любое положение однозначно определяется 3 поворотами вокруг разных осей. Но встаёт вопрос в каком порядке вращать и как выбрать оси?
Обобщённую матрица поворота можно задать по разному. С одной стороны мы можем вращать объект вокруг неподвижных осей. С другой вокруг осей связанных с объектом ещё их называют локальными. Стоит вспомнить что операции умножения матриц не коммутативна поэтому для однозначного определения положения нужно знать не только 3 угла, но и схему умножения матриц.
Можно выделить 2 популярные схемы.
1) Матрица поворота через углы Эйлера.
2) Матрица поворота через углы летательного аппарата (ЛА): рыскание, тангаж и крен(yaw, pitch и roll).
В виду того что первая требует большого числа вычислений, то на практике обычно применяют вторую.
Матрица поворота через углы Эйлера.
Углы Эйлера - три угла однозначно определяющие ориентацию твёрдого тела, определяющие переход от неподвижной системы координат к подвижной.
Подвижная система координат это система координат привязанная к телу. Иногда говорят в мороженная в тело.
Прежде чем дать определения углов нам понадобиться ещё одно.
Линия узлов ON - линия пересечение плоскости OXY и Oxy
α (или φ) это угол между осью Оx и осью ON. Диапазон значений }