Identitné transformácie goniometrických výrazov. Zhrnutie lekcie na tému „Goniometrické výrazy a ich transformácie Príklady goniometrických zjednodušení

Voronková Oľga Ivanovna

MBOU „Stredná škola

č. 18"

Engels, región Saratov.

Učiteľ matematiky.

"Trigonometrické výrazy a ich transformácie"

Úvod …………………………………………………………………………………....3

Kapitola 1 Klasifikácia úloh pre použitie transformácií trigonometrické výrazy ………………………….……………………...5

1.1. Výpočtové úlohy hodnoty goniometrických výrazov……….5

1.2.Úlohy na zjednodušenie goniometrických výrazov .... 7

1.3. Úlohy na prevod číselných goniometrických výrazov ... ..7

1.4 Zmiešané úlohy ……………………………………………………………… 9

Kapitola 2

2.1 Tematické opakovanie v 10. ročníku………………………………………...11

Test 1……………………………………………………………………………………….. 12

Test 2………………………………………………………………………………………..13

Test 3………………………………………………………………………………………..14

2.2 Záverečné opakovanie v 11. ročníku………………………………………………………...15

Test 1……………………………………………………………………………………….. 17

Test 2………………………………………………………………………………………..17

Test 3………………………………………………………………………………………..18

Záver ………………………………………………………………………………………… 19

Zoznam použitej literatúry………………………………………..…….20

Úvod.

V dnešných podmienkach je najdôležitejšia otázka: "Ako môžeme pomôcť odstrániť niektoré medzery vo vedomostiach študentov a varovať ich pred prípadnými chybami na skúške?" Na vyriešenie tohto problému je potrebné od študentov dosiahnuť nie formálnu asimiláciu programového materiálu, ale jeho hlboké a vedomé pochopenie, rozvoj rýchlosti ústnych výpočtov a transformácií, ako aj rozvoj zručností na riešenie najjednoduchších problémy „v mysli“. Je potrebné presvedčiť študentov, že iba ak existuje aktívna pozícia, pri štúdiu matematiky, za predpokladu získania praktických zručností a ich využitia, môžete počítať so skutočným úspechom. Je potrebné využiť každú príležitosť na prípravu na skúšku, vrátane voliteľných predmetov v 10. – 11. ročníku, pravidelne analyzovať zložité úlohy so študentmi, zvoliť najracionálnejší spôsob ich riešenia v triede a mimo vyučovania.pozitívny výsledok voblasť riešenia typických problémov sa dá dosiahnuť, ak učitelia matematiky vytvárajúdobrá základná príprava žiakov, hľadať nové spôsoby riešenia problémov, ktoré sa pred nami otvorili, aktívne experimentovať, aplikovať modernu pedagogické technológie, metódy, techniky, ktoré vytvárajú priaznivé podmienky pre efektívnu sebarealizáciu a sebaurčenie žiakov v nových spoločenských podmienkach.

trigonometria - komponentškolský kurz matematiky. Dobré znalosti a silné zručnosti v trigonometrii sú dôkazom dostatočnej úrovne matematickej kultúry, nevyhnutnou podmienkou úspešného štúdia matematiky, fyziky a mnohých technických disciplín.

Relevantnosť práce. Značná časť absolventov škôl vykazuje z roka na rok veľmi slabú prípravu v tomto dôležitom úseku matematiky, o čom svedčia aj výsledky minulých rokov (percento ukončenia v rokoch 2011-48,41 %, 2012-51,05 %), keďže analýza prob. jednotná štátna skúška ukázala, že študenti pri plnení zadaní z tejto časti robia veľa chýb alebo sa do takýchto zadaní vôbec nepúšťajú. V jednom štátna skúška otázky o trigonometrii sa nachádzajú takmer v troch typoch úloh. Ide o riešenie najjednoduchších goniometrických rovníc v úlohe B5 a prácu s goniometrickými výrazmi v úlohe B7 a štúdium goniometrických funkcií v úlohe B14, ako aj úlohy B12, v ktorých sú vzorce popisujúce fyzikálnych javov a obsahuje goniometrické funkcie. A to je len časť úloh B! Existujú však aj obľúbené trigonometrické rovnice s výberom koreňov C1 a „nie veľmi obľúbené“ geometrické úlohy C2 a C4.

Cieľ. Analyzovať POUŽÍVAJTE materiálúlohy B7, venované transformácii goniometrických výrazov a klasifikovať úlohy podľa formy ich odovzdania v testoch.

Práca pozostáva z dvoch kapitol, úvodu a záveru. V úvode sa zdôrazňuje relevantnosť práce. Prvá kapitola poskytuje klasifikáciu úloh na použitie transformácií goniometrických výrazov v testovacie úlohy POUŽÍVAŤ (2012).

V druhej kapitole sa uvažuje o organizácii opakovania témy "Transformácia goniometrických výrazov" v 10., 11. ročníku a sú vypracované testy na túto tému.

Zoznam použitej literatúry obsahuje 17 zdrojov.

Kapitola 1. Klasifikácia úloh na využitie transformácií goniometrických výrazov.

V súlade so štandardom stredného (úplného) vzdelania a požiadavkami na úroveň prípravy žiakov sú do kodifikátora požiadaviek zaradené úlohy na poznanie základov trigonometrie.

Naučiť sa základy trigonometrie bude najúčinnejšie, keď:

študenti budú pozitívne motivovaní k tomu, aby si zopakovali už preštudovanú látku;

v vzdelávací proces zavedie sa prístup zameraný na človeka;

bude sa uplatňovať systém úloh, ktorý prispieva k rozšíreniu, prehĺbeniu, systematizácii vedomostí žiakov;

budú využívané pokročilé pedagogické technológie.

Po analýze literatúry a internetových zdrojov na prípravu na skúšku sme navrhli jednu z možných klasifikácií úloh B7 (KIM USE 2012-trigonometria): úlohy na výpočethodnoty goniometrických výrazov; úlohy preprevod číselných goniometrických výrazov; úlohy na transformáciu doslovných goniometrických výrazov; zmiešané úlohy.

1.1. Výpočtové úlohy hodnoty goniometrických výrazov.

Jedným z najbežnejších typov jednoduchých problémov s trigonometriou je výpočet hodnôt goniometrických funkcií hodnotou jednej z nich:

a) Použitie základnej goniometrickej identity a jej dôsledkov.

Príklad 1 . Nájdite ak
a
.

rozhodnutie.
,
,

Pretože , potom
.

Odpoveď.

Príklad 2 . Nájsť
, ak
a .

rozhodnutie.
,
,
.

Pretože , potom
.

Odpoveď. .

b) Použitie vzorcov s dvojitým uhlom.

Príklad 3 . Nájsť
, ak
.

rozhodnutie. , .

Odpoveď.
.

Príklad 4 . Nájdite hodnotu výrazu
.

rozhodnutie. .

Odpoveď.
.

1. Nájsť , ak

. Odpoveď. -0,2

2. Nájsť , ak
a
. Odpoveď. 0,4

3. Nájsť

, ak . Odpoveď. -12,884. Nájsť

, ak

. Odpoveď. -0,845. Nájdite hodnotu výrazu:

. Odpoveď. 66. Nájdite hodnotu výrazu

.Odpoveď. - devätnásť

1.2.Úlohy na zjednodušenie goniometrických výrazov. Redukčné vzorce by mali žiaci dobre ovládať, pretože ich ďalej využijú na hodinách geometrie, fyziky a iných príbuzných odborov.

Príklad 5 . Zjednodušte výrazy
.

rozhodnutie. .

Odpoveď.
.

Úlohy na samostatné riešenie:

1. Zjednodušte výraz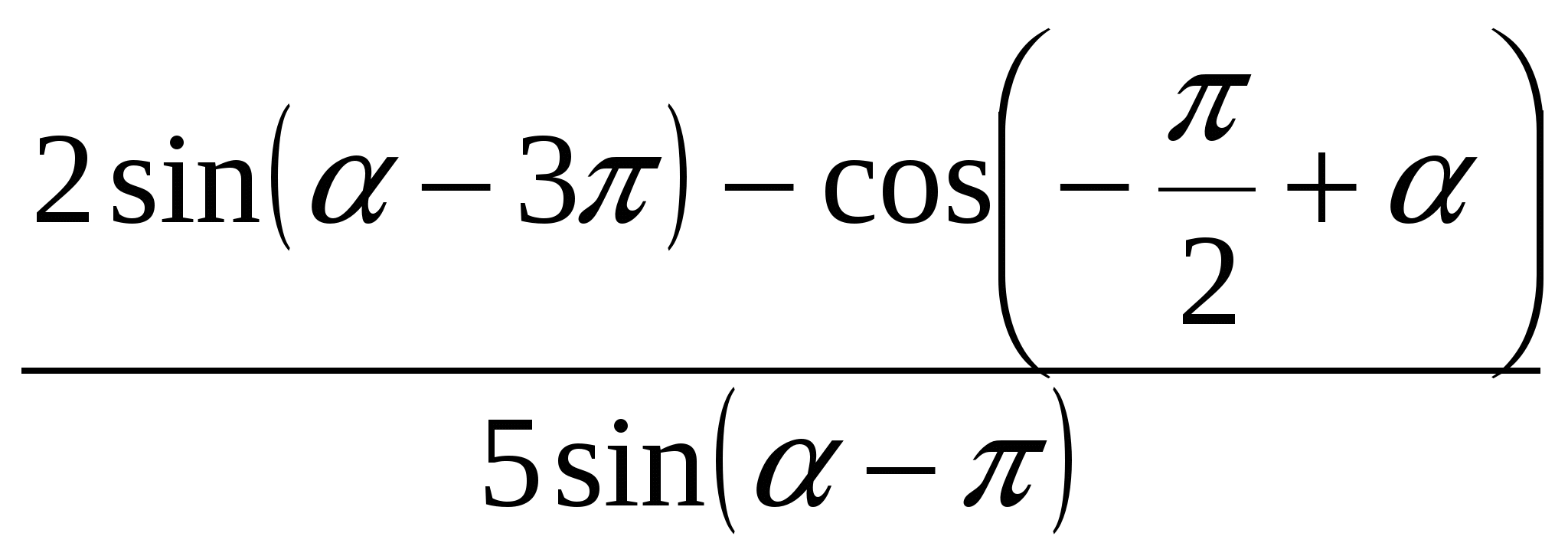

. Odpoveď. 0,62. Nájsť

, ak

a. Odpoveď. 10.563. Nájdite hodnotu výrazu

, ak

. Odpoveď. 2

1.3. Úlohy na transformáciu číselných goniometrických výrazov.

Pri rozvíjaní zručností a schopností úloh na prevod numerických goniometrických výrazov by sa mala venovať pozornosť znalostiam tabuľky hodnôt goniometrických funkcií, vlastnostiam parity a periodicity goniometrických funkcií.

a) Použitie presných hodnôt goniometrických funkcií pre niektoré uhly.

Príklad 6 . Vypočítajte
.

rozhodnutie.
.

Odpoveď.
.

b) Použitie vlastností parity goniometrické funkcie.

Príklad 7 . Vypočítajte
.

rozhodnutie. .

Odpoveď.

v) Použitie vlastností periodicitygoniometrické funkcie.

Príklad 8 . Nájdite hodnotu výrazu
.

rozhodnutie. .

Odpoveď.
.

Úlohy na samostatné riešenie:

1. Nájdite hodnotu výrazu

. Odpoveď. -40,52. Nájdite hodnotu výrazu

. Odpoveď. 17

3. Nájdite hodnotu výrazu
. Odpoveď. 6

. Odpoveď. -24

Odpoveď. -64

1.4 Zmiešané úlohy.

Testovacia forma certifikácie má veľmi výrazné znaky, preto je dôležité venovať pozornosť úlohám spojeným s používaním viacerých goniometrických vzorcov súčasne.

Príklad 9 Nájsť
, ak
.

rozhodnutie.
.

Odpoveď.
.

Príklad 10 . Nájsť
, ak
a
.

rozhodnutie. .

Pretože , potom
.

Odpoveď.
.

Príklad 11. Nájsť
, ak .

rozhodnutie. , ,
,
,
,
,
.

Odpoveď.

Príklad 12. Vypočítajte
.

rozhodnutie. .

Odpoveď.
.

Príklad 13 Nájdite hodnotu výrazu
, ak
.

rozhodnutie. .

Odpoveď.
.

Úlohy na samostatné riešenie:

1. Nájsť

, ak

. Odpoveď. -1,75
2. Nájsť

, ak

. Odpoveď. 33. Nájdite

, ak .Odpoveď. 0,254. Nájdite hodnotu výrazu

, ak

. Odpoveď. 0,35. Nájdite hodnotu výrazu

, ak

. Odpoveď. 5

Kapitola 2. Metodologické aspekty organizácia záverečného opakovania témy "Transformácia goniometrických výrazov."

Jednou z najdôležitejších otázok, ktoré prispievajú k ďalšiemu zlepšovaniu akademických výsledkov, k dosiahnutiu hlbokých a solídnych vedomostí medzi študentmi, je otázka opakovania už preštudovanej látky. Prax ukazuje, že v 10. ročníku je účelnejšie organizovať tematické opakovanie; v 11. ročníku - záverečné opakovanie.

2.1. Tematické opakovanie v 10. ročníku.

V procese práce na matematickom materiáli, najmä veľký význam získava opakovanie každej absolvovanej témy alebo celého úseku kurzu.

Pri tematickom opakovaní sa vedomosti študentov o téme systematizujú v záverečnej fáze jej prechodu alebo po prestávke.

Na tematické opakovanie sú vyčlenené špeciálne hodiny, na ktorých sa sústreďuje a zovšeobecňuje materiál jednej konkrétnej témy.

Opakovanie v lekcii sa uskutočňuje prostredníctvom rozhovoru so širokým zapojením študentov do tohto rozhovoru. Potom dostanú študenti za úlohu zopakovať si určitú tému a sú upozornení, že bude zápočtová práca na testoch.

Test na tému by mal obsahovať všetky jej hlavné otázky. Po dokončení práce sa analyzujú charakteristické chyby a organizuje sa opakovanie na ich odstránenie.

Na lekcie tematického opakovania ponúkame rozvité testovacie papiere na tému „Prevod goniometrických výrazov“.

Test č. 1

Test č. 2

Test č. 3

Tabuľka odpovedí

Test

2.2. Záverečné opakovanie v 11. ročníku.

Záverečné opakovanie sa vykonáva v záverečnej fáze štúdia hlavných problémov kurzu matematiky a vykonáva sa v logickej súvislosti so štúdiom. vzdelávací materiál pre túto sekciu alebo kurz ako celok.

Záverečné opakovanie vzdelávacieho materiálu má tieto ciele:

1. Aktivácia materiálu celku výcvikový kurz objasniť jeho logickú štruktúru a vybudovať systém v rámci predmetových a medzipredmetových vzťahov.

2. Prehlbovanie a podľa možnosti rozširovanie vedomostí študentov o hlavných problémoch predmetu v procese opakovania.

V súvislosti s povinnou skúškou z matematiky pre všetkých absolventov postupné zavádzanie USE núti učiteľov zaujať nový prístup k príprave a vedeniu vyučovacích hodín vzhľadom na potrebu zabezpečiť, aby všetci školáci ovládali vzdelávací materiál na Základná úroveň, ako aj možnosť pre motivovaných študentov, ktorí majú záujem získať vysoké skóre pri nástupe na vysokú školu, dynamicky napredovať v zvládnutí látky na zvýšenej a vysokej úrovni.

V lekciách posledného opakovania môžete zvážiť nasledujúce úlohy:

Príklad 1 . Vypočítajte hodnotu výrazu.rozhodnutie. =

= =

=0,5. Odpoveď. 0,5. Príklad 2 Zadajte najväčšiu celočíselnú hodnotu, ktorú môže výraz nadobudnúť

rozhodnutie. Ako
môže mať akúkoľvek hodnotu patriacu do segmentu [–1; 1], teda
má akúkoľvek hodnotu segmentu [–0,4; 0,4], teda . Celočíselná hodnota výrazu je jedna – číslo 4.

odpoveď: 4 Príklad 3 . Zjednodušte výraz

Riešenie: Použime vzorec na rozklad súčtu kociek: . Máme

Máme:
.

odpoveď: 1

Príklad 4 Vypočítajte
.

rozhodnutie. .

Odpoveď: 0,28

Na hodiny záverečného opakovania ponúkame vypracované testy na tému „Prevod goniometrických výrazov“.

Zadajte najväčšie celé číslo nepresahujúce 1

Záver.

Po vypracovaní relevantného metodickej literatúry na túto tému môžeme konštatovať, že schopnosť a zručnosti riešiť úlohy súvisiace s goniometrickými transformáciami v školský kurz matematika je veľmi dôležitá.

V rámci vykonaných prác bola vykonaná klasifikácia úloh B7. Zohľadňujú sa trigonometrické vzorce najčastejšie používané v CMM z roku 2012. Uvádzajú sa príklady úloh s riešeniami. Na organizáciu opakovania a systematizácie vedomostí pri príprave na skúšku boli vyvinuté diferencovateľné testy.

Je vhodné pokračovať v začatej práci, zvažovať riešenie najjednoduchších goniometrických rovníc v úlohe B5, náuka o goniometrických funkciách v úlohe B14, v úlohe B12, v ktorých sú vzorce popisujúce fyzikálne javy a obsahujúce goniometrické funkcie.

Na záver by som chcel poznamenať, že účinnosť absolvovanie skúšky je do značnej miery determinované tým, ako efektívne je zorganizovaný tréningový proces na všetkých stupňoch vzdelávania, so všetkými kategóriami žiakov. A ak sa nám podarí formovať u žiakov samostatnosť, zodpovednosť a pripravenosť pokračovať v učení po celý ich ďalší život, naplníme tým nielen príkazy štátu a spoločnosti, ale aj zvýšime vlastnú sebaúctu.

Opakovanie vzdelávacieho materiálu vyžaduje učiteľa tvorivá práca. Musí poskytnúť jasné spojenie medzi typmi opakovania, implementovať hlboko premyslený systém opakovania. Zvládnuť umenie organizovať opakovanie je úlohou učiteľa. Sila vedomostí žiakov do značnej miery závisí od jej riešenia.

Literatúra.

Vygodsky Ya.Ya., Príručka elementárnej matematiky. -M.: Nauka, 1970.

Úlohy vyššej náročnosti v algebre a začiatky analýzy: Učebnica pre ročníky 10-11 stredná škola/ B.M. Ivlev, A.M. Abramov, Yu.P. Dudnitsyn, S.I. Schwarzburd. – M.: Osveta, 1990.

Aplikácia základných goniometrických vzorcov na transformáciu výrazov (10. ročník) // Festival pedagogických nápadov. 2012-2013.

Koryanov A.G. , Prokofiev A.A. Na skúšku pripravujeme dobrých študentov a výborných študentov. - M.: Vysoká škola pedagogická "Prvý september", 2012.- 103 s.

Kuznecovová E.N. Zjednodušenie goniometrických výrazov. Riešenie goniometrických rovníc rôznymi metódami (príprava na skúšku). 11. trieda. 2012-2013.

Kulanin E.D. 3000 konkurenčných problémov v matematike. 4. id., správne. a dodatočné – M.: Rolf, 2000.

Mordkovich A.G. Metodické problémy štúdia trigonometrie na všeobecnovzdelávacej škole // Matematika v škole. 2002. Číslo 6.

Pichurin L.F. O trigonometrii a nielen o nej: -M. Osvietenstvo, 1985

Rešetnikov N.N. Trigonometria v škole: -M. : Vysoká škola pedagogická "Prvý september", 2006, lk 1.

Shabunin M.I., Prokofiev A.A. Matematika. Algebra. Začiatky matematickej analýzy Profilová úroveň: učebnica pre ročník 10 - M .: BINOM. Knowledge Lab, 2007.

Vzdelávací portál na prípravu na skúšku.

Príprava na skúšku z matematiky „Ach, táto trigonometria! http://festival.1september.ru/articles/621971/

Projekt "Matematika? Ľahko!!!" http://www.resolventa.ru/

AT identické premeny trigonometrické výrazy možno použiť nasledujúce algebraické triky: sčítanie a odčítanie rovnakých pojmov; vyňatie spoločného činiteľa zo zátvoriek; násobenie a delenie rovnakou hodnotou; aplikácia skrátených vzorcov násobenia; výber celého štvorca; faktorizácia štvorcového trojčlenu; zavedenie nových premenných na zjednodušenie transformácií.

Pri prevode goniometrických výrazov obsahujúcich zlomky môžete využiť vlastnosti podielu, zmenšenia zlomkov alebo zmenšenia zlomkov na spoločného menovateľa. Okrem toho môžete použiť výber celočíselnej časti zlomku, vynásobenie čitateľa a menovateľa zlomku rovnakou hodnotou a tiež, ak je to možné, vziať do úvahy jednotnosť čitateľa alebo menovateľa. V prípade potreby môžete zlomok reprezentovať ako súčet alebo rozdiel niekoľkých jednoduchších zlomkov.

Okrem toho pri použití všetkých potrebných metód na prevod goniometrických výrazov je potrebné neustále brať do úvahy rozsah prípustných hodnôt prevedených výrazov.

Pozrime sa na pár príkladov.

Príklad 1

Vypočítajte A = (sin (2x - π) cos (3π - x) + sin (2x - 9π/2) cos (x + π/2)) 2 + (cos (x - π/2) cos ( 2x – 7π /2) +
+ hriech (3π/2 - x) hriech (2x -5π/2)) 2

rozhodnutie.

Z redukčných vzorcov to vyplýva:

sin (2x - π) \u003d -sin 2x; cos (3π - x) \u003d -cos x;

hriech (2x - 9π / 2) \u003d -cos 2x; cos (x + π/2) = -sin x;

cos (x - π / 2) \u003d sin x; cos (2x - 7π/2) = -sin 2x;

sin (3π / 2 - x) \u003d -cos x; hriech (2x - 5π / 2) \u003d -cos 2x.

Odkiaľ na základe vzorcov na sčítanie argumentov a základnej goniometrickej identity získame

A \u003d (sin 2x cos x + cos 2x sin x) 2 + (-sin x sin 2x + cos x cos 2x) 2 \u003d sin 2 (2x + x) + cos 2 (x + 2x) \u003d
= hriech 2 3x + cos 2 3x = 1

odpoveď: 1.

Príklad 2

Premeňte výraz M = cos α + cos (α + β) cos γ + cos β – sin (α + β) sin γ + cos γ na súčin.

rozhodnutie.

Zo vzorcov na sčítanie argumentov a vzorcov na prevod súčtu goniometrických funkcií na súčin po príslušnom zoskupení máme

М = (cos (α + β) cos γ - sin (α + β) sin γ) + cos α + (cos β + cos γ) =

2cos ((β + γ)/2) cos ((β – γ)/2) + (cos α + cos (α + β + γ)) =

2cos ((β + γ)/2) cos ((β – γ)/2) + 2cos (α + (β + γ)/2) cos ((β + γ)/2)) =

2cos ((β + γ)/2) (cos ((β – γ)/2) + cos (α + (β + γ)/2)) =

2cos ((β + γ)/2) 2cos ((β – γ)/2 + α + (β + γ)/2)/2) cos ((β – γ)/2) – (α + ( β + γ)/2)/2) =

4cos ((β + γ)/2) cos ((α + β)/2) cos ((α + γ)/2).

Odpoveď: М = 4cos ((α + β)/2) cos ((α + γ)/2) cos ((β + γ)/2).

Príklad 3.

Ukážte, že výraz A \u003d cos 2 (x + π / 6) - cos (x + π / 6) cos (x - π / 6) + cos 2 (x - π / 6) platí pre všetky x z R jedna a rovnakú hodnotu. Nájdite túto hodnotu.

rozhodnutie.

Ponúkame dva spôsoby riešenia tohto problému. Aplikovaním prvej metódy, izoláciou celého štvorca a použitím zodpovedajúcich základných goniometrických vzorcov, získame

A \u003d (cos (x + π / 6) - cos (x - π / 6)) 2 + cos (x - π / 6) cos (x - π / 6) \u003d

4sin 2 x sin 2 π/6 + 1/2 (cos 2x + cos π/3) =

Hriech 2 x + 1/2 cos 2x + 1/4 = 1/2 (1 - cos 2x) + 1/2 cos 2x + 1/4 = 3/4.

Pri riešení úlohy druhým spôsobom uvažujte A ako funkciu x z R a vypočítajte jej deriváciu. Po transformáciách dostaneme

А´ \u003d -2cos (x + π/6) sin (x + π/6) + (sin (x + π/6) cos (x - π/6) + cos (x + π/6) sin ( x + π/6)) - 2cos (x - π/6) sin (x - π/6) =

Sin 2(x + π/6) + sin ((x + π/6) + (x - π/6)) - sin 2(x - π/6) =

Hriech 2x - (hriech (2x + π/3) + hriech (2x - π/3)) =

Sin 2x - 2sin 2x cos π/3 = hriech 2x - sin 2x ≡ 0.

Na základe kritéria stálosti funkcie diferencovateľnej na intervale sme teda dospeli k záveru, že

A(x) ≡ (0) = cos 2 π/6 - cos 2 π/6 + cos 2 π/6 = (√3/2) 2 = 3/4, x ∈ R.

Odpoveď: A = 3/4 za x € R.

Hlavné metódy dokazovania goniometrickej identity sú:

a) redukcia ľavej strany identity na pravú stranu vhodnými transformáciami;
b) zmenšenie pravej strany identity na ľavú;
v) redukcia pravej a ľavej časti identity na rovnakú formu;
G) zníženie rozdielu medzi ľavou a pravou časťou preukazovanej totožnosti na nulu.

Príklad 4

Skontrolujte, či cos 3x = -4cos x cos (x + π/3) cos (x + 2π/3).

rozhodnutie.

Transformáciu pravej strany tejto identity podľa zodpovedajúcich goniometrických vzorcov máme

4cos x cos (x + π/3) cos (x + 2π/3) =

2cos x (cos ((x + π/3) + (x + 2π/3)) + cos ((x + π/3) – (x + 2π/3))) =

2cos x (cos (2x + π) + cos π/3) =

2cos x cos 2x - cos x = (cos 3x + cos x) - cos x = cos 3x.

Pravá strana identity je zredukovaná na ľavú stranu.

Príklad 5

Dokážte, že sin 2 α + sin 2 β + sin 2 γ – 2cos α cos β cos γ = 2, ak α, β, γ sú vnútorné uhly nejakého trojuholníka.

rozhodnutie.

Ak vezmeme do úvahy, že α, β, γ sú vnútorné uhly nejakého trojuholníka, dostaneme to

α + β + γ = π a teda γ = π – α – β.

sin 2 α + sin 2 β + sin 2 γ – 2cos α cos β cos γ =

Sin 2 α + sin 2 β + sin 2 (π - α - β) - 2cos α cos β cos (π - α - β) =

Sin 2 α + sin 2 β + sin 2 (α + β) + (cos (α + β) + cos (α - β) (cos (α + β) =

Sin 2 α + sin 2 β + (sin 2 (α + β) + cos 2 (α + β)) + cos (α - β) (cos (α + β) =

1/2 (1 – cos 2α) + ½ (1 – cos 2β) + 1 + 1/2 (cos 2α + cos 2β) = 2.

Pôvodná rovnosť je dokázaná.

Príklad 6

Dokážte, že na to, aby sa jeden z uhlov α, β, γ trojuholníka rovnal 60°, je potrebné a postačujúce, aby sin 3α + sin 3β + sin 3γ = 0.

rozhodnutie.

Podmienka tohto problému predpokladá dôkaz nevyhnutnosti aj dostatočnosti.

Najprv dokazujeme potrebu.

Dá sa to ukázať

sin 3α + sin 3β + sin 3γ = -4cos (3α/2) cos (3β/2) cos (3γ/2).

Ak teda vezmeme do úvahy, že cos (3/2 60°) = cos 90° = 0, dostaneme, že ak sa jeden z uhlov α, β alebo γ rovná 60°, potom

cos (3α/2) cos (3β/2) cos (3γ/2) = 0 a teda sin 3α + sin 3β + sin 3γ = 0.

Teraz dokážme primeranosťšpecifikovaný stav.

Ak sin 3α + sin 3β + sin 3γ = 0, potom cos (3α/2) cos (3β/2) cos (3γ/2) = 0, a preto

buď cos (3α/2) = 0, alebo cos (3β/2) = 0, alebo cos (3γ/2) = 0.

teda

alebo 3α/2 = π/2 + πk, t.j. α = π/3 + 2πk/3,

alebo 3β/2 = π/2 + πk, t.j. β = π/3 + 2πk/3,

alebo 3γ/2 = π/2 + πk,

tie. γ = π/3 + 2πk/3, kde k ϵ Z.

Zo skutočnosti, že α, β, γ sú uhly trojuholníka, máme

0 < α < π, 0 < β < π, 0 < γ < π.

Preto pre α = π/3 + 2πk/3 alebo β = π/3 + 2πk/3 resp.

γ = π/3 + 2πk/3 zo všetkých kϵZ vyhovuje iba k = 0.

Z toho vyplýva, že buď α = π/3 = 60°, alebo β = π/3 = 60°, alebo γ = π/3 = 60°.

Tvrdenie bolo dokázané.

Máte nejaké otázky? Neviete ako zjednodušiť trigonometrické výrazy?
Ak chcete získať pomoc tútora - zaregistrujte sa.
Prvá lekcia je zadarmo!

stránky, s úplným alebo čiastočným kopírovaním materiálu, je potrebný odkaz na zdroj.

Sekcie: Matematika

Trieda: 11

Lekcia 1

Predmet: 11. ročník (príprava na skúšku)

Zjednodušenie goniometrických výrazov.

Riešenie najjednoduchších goniometrických rovníc. (2 hodiny)

Ciele:

Systematizovať, zovšeobecňovať, rozširovať vedomosti a zručnosti žiakov súvisiace s používaním trigonometrických vzorcov a riešením najjednoduchších goniometrických rovníc.

Vybavenie na lekciu:

Štruktúra lekcie:

Orgmoment
Testovanie na notebookoch. Diskusia o výsledkoch.
Zjednodušenie goniometrických výrazov
Riešenie najjednoduchších goniometrických rovníc
Samostatná práca.
Zhrnutie lekcie. Vysvetlenie domácej úlohy.

1. Organizačný moment. (2 minúty.)

Učiteľ privíta poslucháčov, oznámi tému hodiny, pripomenie, že predtým bola zadaná úloha zopakovať trigonometrické vzorce a pripraví žiakov na testovanie.

2. Testovanie. (15 minút + 3 minúty diskusia)

Cieľom je preveriť znalosti goniometrických vzorcov a schopnosť ich aplikovať. Každý študent má na stole notebook, v ktorom je možnosť testovania.

Môže existovať ľubovoľný počet možností, uvediem príklad jednej z nich:

I možnosť.

Zjednodušte výrazy:

a) základné trigonometrické identity

1. sin 2 3y + cos 2 3y + 1;

b) adičné vzorce

3. hriech5x - hriech3x;

c) prevod produktu na sumu

6. 2sin8y cos3y;

d) vzorce dvojitého uhla

7,2 sin5x cos5x;

e) vzorce polovičného uhla

f) vzorce trojitého uhla

g) univerzálna substitúcia

h) zníženie stupňa

16. cos 2 (3x/7);

Študenti na notebooku pred každým vzorcom vidia svoje odpovede.

Práca je okamžite kontrolovaná počítačom. Výsledky sa zobrazia na veľkej obrazovke pre každého.

Taktiež po skončení práce sa správne odpovede zobrazujú žiakom na notebookoch. Každý žiak vidí, kde sa stala chyba a aké vzorce potrebuje zopakovať.

3. Zjednodušenie goniometrických výrazov. (25 min.)

Cieľom je zopakovať, vypracovať a upevniť aplikáciu základných vzorcov trigonometrie. Riešenie úloh B7 zo skúšky.

V tejto fáze je vhodné rozdeliť triedu do skupín silných (pracovať samostatne s následným overením) a slabí žiaci ktorí spolupracujú s učiteľom.

Zadanie pre silných študentov (pripravené vopred na tlačenom základe). Hlavný dôraz sa kladie na vzorce zmenšenia a dvojitého uhla podľa USE 2011.

Zjednodušte výrazy (pre silných študentov):

Paralelne učiteľ pracuje so slabými žiakmi, diskutuje a rieši úlohy na obrazovke pod diktátom žiakov.

Vypočítať:

5) sin (270º - α) + cos (270º + α)

Zjednodušiť:

Na rad prišla diskusia o výsledkoch práce silnej skupiny.

Odpovede sa zobrazia na obrazovke a tiež pomocou videokamery sa zobrazia práce 5 rôznych študentov (pre každého jedna úloha).

Slabá skupina vidí podmienku a spôsob riešenia. Existuje diskusia a analýza. S využitím technických prostriedkov sa to deje rýchlo.

4. Riešenie najjednoduchších goniometrických rovníc. (30 min.)

Cieľom je zopakovať, systematizovať a zovšeobecniť riešenie najjednoduchších goniometrických rovníc so zaznamenaním ich koreňov. Riešenie úlohy B3.

Akákoľvek goniometrická rovnica, bez ohľadu na to, ako ju vyriešime, vedie k najjednoduchšej.

Žiaci by pri plnení úlohy mali venovať pozornosť písaniu koreňov rovníc špeciálnych prípadov a všeobecný pohľad a o výbere koreňov v poslednej rovnici.

Riešiť rovnice:

Napíšte najmenší kladný koreň odpovede.

5. Samostatná práca (10 min.)

Cieľom je otestovať nadobudnuté zručnosti, identifikovať problémy, chyby a spôsoby ich odstránenia.

Podľa výberu študenta sú ponúkané rôzne práce.

Možnosť pre "3"

1) Nájdite hodnotu výrazu

2) Zjednodušte výraz 1 - sin 2 3α - cos 2 3α

3) Vyriešte rovnicu

Možnosť pre "4"

1) Nájdite hodnotu výrazu

2) Vyriešte rovnicu Napíšte najmenší kladný koreň svojej odpovede.

Možnosť pre "5"

1) Nájdite tgα, ak

2) Nájdite koreň rovnice Napíšte najmenší kladný koreň svojej odpovede.

6. Zhrnutie hodiny (5 min.)

Učiteľ zhŕňa skutočnosť, že hodina zopakovala a upevnila goniometrické vzorce, riešenie najjednoduchších goniometrických rovníc.

Dané domáca úloha(vopred pripravené na tlačenej báze) s náhodnou kontrolou na nasledujúcej lekcii.

Riešiť rovnice:

10) Uveďte svoju odpoveď ako najmenší kladný koreň.

lekcia 2

Predmet: 11. ročník (príprava na skúšku)

Metódy riešenia goniometrických rovníc. Výber koreňa. (2 hodiny)

Ciele:

Zovšeobecniť a systematizovať poznatky o riešení goniometrických rovníc rôznych typov.
Podporovať rozvoj matematického myslenia žiakov, schopnosť pozorovať, porovnávať, zovšeobecňovať, klasifikovať.
Povzbudzovať žiakov k prekonávaniu ťažkostí v procese duševnej činnosti, k sebakontrole, introspekcii svojich činností.

Vybavenie na lekciu: KRMu, notebooky pre každého študenta.

Štruktúra lekcie:

Orgmoment
Diskusia d/sa samot. práca z poslednej lekcie
Opakovanie metód riešenia goniometrických rovníc.
Riešenie goniometrických rovníc
Výber koreňov v goniometrických rovniciach.
Samostatná práca.
Zhrnutie lekcie. Domáca úloha.

1. Organizačný moment (2 min.)

Učiteľ pozdraví poslucháčov, oznámi tému hodiny a plán práce.

2. a) Rozbor domácej úlohy (5 min.)

Cieľom je skontrolovať výkon. Jedno dielo pomocou videokamery sa zobrazí na obrazovke, ostatné sa selektívne zbierajú, aby ich učiteľ skontroloval.

b) Analýza samostatnej práce (3 min.)

Cieľom je vyriešiť chyby, naznačiť spôsoby, ako ich prekonať.

Na obrazovke sú odpovede a riešenia, študenti vopred vydali svoje práce. Analýza prebieha rýchlo.

3. Opakovanie metód riešenia goniometrických rovníc (5 min.)

Cieľom je pripomenúť si metódy riešenia goniometrických rovníc.

Opýtajte sa žiakov, aké metódy riešenia goniometrických rovníc poznajú. Zdôraznite, že existujú takzvané základné (často používané) metódy:

variabilná substitúcia,
faktorizácia,
homogénne rovnice,

a tam sú použité metódy:

podľa vzorcov na prepočet sumy na súčin a súčinu na súčet,
podľa redukčných vzorcov,
univerzálna trigonometrická substitúcia
zavedenie pomocného uhla,
násobenie niekt goniometrická funkcia.

Treba tiež pripomenúť, že jedna rovnica môže byť vyriešená rôznymi spôsobmi.

4. Riešenie goniometrických rovníc (30 min.)

Cieľom je zovšeobecniť a upevniť vedomosti a zručnosti na túto tému, pripraviť sa na riešenie C1 z USE.

Považujem za účelné riešiť rovnice pre každú metódu spolu so žiakmi.

Žiak nadiktuje riešenie, učiteľ zapíše na tablet, celý postup sa zobrazí na obrazovke. To vám umožní rýchlo a efektívne obnoviť predtým pokrytý materiál vo vašej pamäti.

Riešiť rovnice:

1) zmena premennej 6cos 2 x + 5sinx - 7 = 0

2) faktorizácia 3cos(x/3) + 4cos 2 (x/3) = 0

3) homogénne hriechové rovnice 2x + 3cos 2x - 2sin2x = 0

4) prevod súčtu na súčin cos5x + cos7x = cos(π + 6x)

5) prevod produktu na súčet 2sinx sin2x + cos3x = 0

6) zníženie stupňa sin2x - sin 2 2x + sin 2 3x \u003d 0,5

7) univerzálna trigonometrická substitúcia sinx + 5cosx + 5 = 0.

Pri riešení tejto rovnice je potrebné poznamenať, že použitie tejto metódy vedie k zúženiu oblasti definície, pretože sínus a kosínus sú nahradené tg(x/2). Preto pred napísaním odpovede musíte skontrolovať, či čísla z množiny π + 2πn, n Z sú koňmi tejto rovnice.

8) zavedenie pomocného uhla √3sinx + cosx - √2 = 0

9) násobenie nejakou goniometrickou funkciou cosx cos2x cos4x = 1/8.

5. Výber koreňov goniometrických rovníc (20 min.)

Keďže v podmienkach tvrdej konkurencie pri nástupe na vysoké školy nestačí riešenie jednej prvej časti skúšky, väčšina študentov by mala venovať pozornosť úlohám druhej časti (C1, C2, C3).

Účelom tejto fázy lekcie je preto pripomenúť si predtým preštudovaný materiál, pripraviť sa na riešenie problému C1 z USE v roku 2011.

Existujú trigonometrické rovnice, v ktorých musíte pri písaní odpovede vybrať korene. Je to spôsobené niektorými obmedzeniami, napríklad: menovateľ zlomku sa nerovná nule, výraz pod odmocninou párneho stupňa je nezáporný, výraz pod znamienkom logaritmu je kladný atď.

Takéto rovnice sú považované za rovnice so zvýšenou zložitosťou a vo verzii USE sú v druhej časti, konkrétne C1.

Vyriešte rovnicu:

Zlomok je nula, ak potom pomocou jednotkového kruhu vyberieme korene (pozri obrázok 1)

Obrázok 1.

dostaneme x = π + 2πn, n Z

Odpoveď: π + 2πn, n Z

Na obrazovke je výber koreňov zobrazený v kruhu na farebnom obrázku.

Súčin sa rovná nule, keď sa aspoň jeden z faktorov rovná nule a oblúk zároveň nestráca svoj význam. Potom

Pomocou jednotkového kruhu vyberte korene (pozri obrázok 2)

Video lekcia „Zjednodušenie goniometrických výrazov“ je určená na formovanie zručností žiakov pri riešení goniometrických úloh pomocou základných goniometrických identít. Počas video lekcie sa zvažujú typy goniometrických identít, príklady riešenia problémov pomocou nich. Pomocou názorných pomôcok je pre učiteľa jednoduchšie dosiahnuť ciele hodiny. Živá prezentácia materiálu prispieva k zapamätaniu dôležitých bodov. Použitie animačných efektov a hlasového prejavu vám umožňuje úplne nahradiť učiteľa vo fáze vysvetľovania látky. Využitím tejto názornej pomôcky na hodinách matematiky môže učiteľ zvýšiť efektivitu vyučovania.

Na začiatku video lekcie je oznámená jej téma. Potom sa vybavia skôr študované trigonometrické identity. Na obrazovke sa zobrazia rovnosti sin 2 t+cos 2 t=1, tg t=sin t/cos t, kde t≠π/2+πk pre kϵZ, ctg t=cos t/sin t, platí pre t≠πk, kde kϵZ, tan t · ctg t=1, pri t≠πk/2, kde kϵZ, nazývané základné goniometrické identity. Je potrebné poznamenať, že tieto identity sa často používajú pri riešení problémov, kde je potrebné dokázať rovnosť alebo zjednodušiť výraz.

Ďalej sú zvažované príklady použitia týchto identít pri riešení problémov. Najprv sa navrhuje zvážiť riešenie problémov so zjednodušením výrazov. V príklade 1 je potrebné zjednodušiť výraz cos 2 t- cos 4 t+ sin 4 t. Ak chcete vyriešiť príklad, najprv zadajte zátvorku spoločný faktor cena 2 t. V dôsledku takejto transformácie v zátvorke dostaneme výraz 1-cos 2 t, ktorého hodnota zo základnej identity trigonometrie sa rovná sin 2 t. Po transformácii výrazu je zrejmé, že zo zátvoriek možno vyňať ešte jeden spoločný činiteľ sin 2 t, po ktorom výraz nadobúda tvar sin 2 t (sin 2 t + cos 2 t). Z rovnakej základnej identity odvodíme hodnotu výrazu v zátvorkách rovnú 1. Zjednodušením dostaneme cos 2 t- cos 4 t+ sin 4 t= sin 2 t.

V príklade 2 je tiež potrebné zjednodušiť výraz náklady/(1- sint)+ náklady/(1+ sint). Keďže cena výrazu je v čitateloch oboch zlomkov, možno ju vymedziť ako spoločný faktor. Potom sa zlomky v zátvorkách zredukujú na spoločného menovateľa vynásobením (1- sint) (1+ sint). Po uvedení podobných pojmov v čitateli zostáva 2 a v menovateli 1 - hriech 2 t. Na pravej strane obrazovky sa zobrazí základná trigonometrická identita sin 2 t+cos 2 t=1. Pomocou neho nájdeme menovateľ zlomku cos 2 t. Po zmenšení zlomku dostaneme zjednodušenú formu výrazu cena / (1- sint) + cena / (1 + sint) \u003d 2 / cena.

Ďalej uvažujeme o príkladoch dokazovania identít, v ktorých sa uplatňujú získané poznatky o základných identitách trigonometrie. V príklade 3 je potrebné preukázať totožnosť (tg 2 t-sin 2 t)·ctg 2 t=sin 2 t. Pravá strana obrazovky zobrazuje tri identity, ktoré budú potrebné na dôkaz - tg t ctg t=1, ctg t=cos t/sin t a tg t=sin t/cc t s obmedzeniami. Na preukázanie identity sa najprv otvoria zátvorky, potom sa vytvorí súčin, ktorý odráža vyjadrenie hlavnej goniometrickej identity tg t·ctg t=1. Potom sa podľa identity z definície kotangens transformuje ctg 2 t. V dôsledku transformácií sa získa výraz 1-cos 2 t. Pomocou základnej identity nájdeme hodnotu výrazu. Je teda dokázané, že (tg 2 t-sin 2 t)·ctg 2 t=sin 2 t.

V príklade 4 musíte nájsť hodnotu výrazu tg 2 t+ctg 2 t, ak tg t+ctg t=6. Na vyhodnotenie výrazu sa pravá a ľavá strana rovnice (tg t+ctg t) 2 =6 2 najprv odmocní. Skrátený vzorec násobenia sa zobrazuje na pravej strane obrazovky. Po otvorení zátvoriek na ľavej strane výrazu vznikne súčet tg 2 t+2 tg t ctg t+ctg 2 t, na transformáciu ktorého možno použiť jednu z goniometrických identít tg t ctg t=1, ktorého forma je vyvolaná na pravej strane obrazovky. Po transformácii sa získa rovnosť tg2t+ctg2t=34. Ľavá strana rovnosti sa zhoduje s podmienkou úlohy, takže odpoveď je 34. Úloha je vyriešená.

Video lekcia „Zjednodušenie goniometrických výrazov“ sa odporúča použiť na tradičnej školskej hodine matematiky. Materiál bude užitočný aj pre učiteľa, ktorý poskytuje dištančné vzdelávanie. S cieľom vytvoriť zručnosť pri riešení goniometrických problémov.

INTERPRETÁCIA TEXTU:

„Zjednodušenie goniometrických výrazov“.

Rovnosť

1) sin 2 t + cos 2 t = 1 (sínusová druhá mocnina te plus kosínusová druhá mocnina te sa rovná jednej)

2) tgt =, pri t ≠ + πk, kϵZ (tangens te sa rovná pomeru sínusu te ku kosínusu te, keď te sa nerovná pi o dva plus pi ka, ka patrí k zet)

3) ctgt = , pri t ≠ πk, kϵZ (kotangens te sa rovná pomeru kosínusu te k sínusu te, keď sa te nerovná vrcholu ka, ktorý patrí do z).

4) tgt ∙ ctgt = 1 pri t ≠ , kϵZ

sa nazývajú základné goniometrické identity.

Často sa používajú pri zjednodušovaní a dokazovaní goniometrických výrazov.

Zvážte príklady použitia týchto vzorcov pri zjednodušovaní goniometrických výrazov.

PRÍKLAD 1. Zjednodušte výraz: cos 2 t - cos 4 t + sin 4 t. (výraz kosínusová druhá mocnina te mínus kosínus štvrtého stupňa te plus sínus štvrtého stupňa te).

rozhodnutie. cos 2 t - cos 4 t + sin 4 t = cos 2 t∙ (1 - cos 2 t) + sin 4 t = cos 2 t ∙ sin 2 t + sin 4 t = sin 2 t (cos 2 t + sin 2 t) = hriech 2 t 1 = hriech 2 t

(vyberieme spoločný činiteľ kosínusová kvadráta te, v zátvorkách dostaneme rozdiel medzi jednotou a druhou mocninou kosínusového te, ktorý sa rovná druhej mocnine sínusu te pri prvej identite. Dostaneme súčet sínusov štvrtého stupeň te súčinu kosínusovej kvadráty te a sínusovej kvadráty te Spoločný činiteľ sínusová kvadráta te vyjmeme mimo zátvorky, v zátvorkách dostaneme súčet druhých mocnín kosínusu a sínusu, ktorý podľa základnej goniometrické identity, sa rovná 1. V dôsledku toho dostaneme druhú mocninu sínusu te).

PRÍKLAD 2. Zjednodušte výraz: + .

(výraz je súčet dvoch zlomkov v čitateli prvého kosínusu te v menovateli jedna mínus sínus te, v čitateli druhého kosínusu te v menovateli druhého plus sínus te).

(Vyberme spoločný činiteľ kosínus te zo zátvoriek a v zátvorkách ho uveďte do spoločného menovateľa, ktorý je súčinom jedného mínus sínus te a jedného plus sínus te.

V čitateli dostaneme: jeden plus sínus te plus jeden mínus sínus te, dáme podobné, v čitateli sa po prinesení podobných rovná dvom.

V menovateli môžete použiť skrátený vzorec násobenia (rozdiel druhých mocnín) a získať rozdiel medzi jednotkou a druhou mocninou sínusu te, ktorý podľa základnej goniometrickej identity

sa rovná druhej mocnine kosínusu te. Po zmenšení o kosínus te dostaneme konečnú odpoveď: dve delené kosínusom te).

Zvážte príklady použitia týchto vzorcov pri dôkaze goniometrických výrazov.

PRÍKLAD 3. Dokážte totožnosť (tg 2 t - sin 2 t) ∙ ctg 2 t \u003d sin 2 t (súčin rozdielu medzi druhou mocninou tangens te a sínusom te a druhou mocninou kotangensu te sa rovná druhej mocnine sínusu te).

Dôkaz.

Transformujme ľavú stranu rovnosti:

(tg 2 t - sin 2 t) ∙ ctg 2 t = tg 2 t ∙ ctg 2 t - sin 2 t ∙ ctg 2 t = 1 - sin 2 t ∙ ctg 2 t =1 - sin 2 t 1 - cos 2 t = hriech 2 t

(Otvorme zátvorky, z predtým získaného vzťahu je známe, že súčin druhých mocnín tangenta te kotangensom te sa rovná jednej. Pripomeňme, že kotangens te sa rovná podielu kosínusu te k sínusu te, čo znamená, že druhá mocnina kotangensu je pomer druhej mocniny kosínusu te k druhej mocnine sínusu te.

Po zmenšení o sínusovú druhú mocninu te dostaneme rozdiel medzi jednotkou a kosínusom druhej mocniny te, ktorý sa rovná sínusu druhej mocniny te). Q.E.D.

PRÍKLAD 4. Nájdite hodnotu výrazu tg 2 t + ctg 2 t, ak tgt + ctgt = 6.

(súčet druhých mocnín tangensu te a kotangensu te, ak súčet tangensu a kotangensu je šesť).

rozhodnutie. (tgt + ctgt) 2 = 6 2

tg 2 t + 2 ∙ tgt ∙ ctgt + ctg 2 t = 36

tg2t + 2 + ctg2t = 36

tg2t + ctg2t = 36-2

tg2t + ctg2t = 34

Odmocnime obe časti pôvodnej rovnosti:

(tgt + ctgt) 2 = 6 2 (druhá mocnina súčtu tangens te a kotangens te je šesť na druhú). Pripomeňme si skrátený vzorec na násobenie: Druhá mocnina súčtu dvoch veličín sa rovná druhej mocnine prvej plus dvojnásobku súčinu prvej a druhej plus druhej mocniny druhej. (a+b) 2 =a 2 +2ab+b 2 Dostaneme tg 2 t + 2 ∙ tgt ∙ctgt + ctg 2 t = 36 .

Pretože súčin tangens te a kotangens te sa rovná jednej, potom tg 2 t + 2 + ctg 2 t \u003d 36 (súčet druhých mocnín tangens te a kotangens te a dva je tridsaťšesť),

Sekcie: Matematika

Trieda: 11

Lekcia 1

Predmet: 11. ročník (príprava na skúšku)

Zjednodušenie goniometrických výrazov.

Riešenie najjednoduchších goniometrických rovníc. (2 hodiny)

Ciele:

Systematizovať, zovšeobecňovať, rozširovať vedomosti a zručnosti žiakov súvisiace s používaním trigonometrických vzorcov a riešením najjednoduchších goniometrických rovníc.

Vybavenie na lekciu:

Štruktúra lekcie:

Orgmoment
Testovanie na notebookoch. Diskusia o výsledkoch.
Zjednodušenie goniometrických výrazov
Riešenie najjednoduchších goniometrických rovníc
Samostatná práca.
Zhrnutie lekcie. Vysvetlenie domácej úlohy.

1. Organizačný moment. (2 minúty.)

Učiteľ privíta poslucháčov, oznámi tému hodiny, pripomenie, že predtým bola zadaná úloha zopakovať trigonometrické vzorce a pripraví žiakov na testovanie.

2. Testovanie. (15 minút + 3 minúty diskusia)

Cieľom je preveriť znalosti goniometrických vzorcov a schopnosť ich aplikovať. Každý študent má na stole notebook, v ktorom je možnosť testovania.

Môže existovať ľubovoľný počet možností, uvediem príklad jednej z nich:

I možnosť.

Zjednodušte výrazy:

a) základné trigonometrické identity

1. sin 2 3y + cos 2 3y + 1;

b) adičné vzorce

3. hriech5x - hriech3x;

c) prevod produktu na sumu

6. 2sin8y cos3y;

d) vzorce dvojitého uhla

7,2 sin5x cos5x;

e) vzorce polovičného uhla

f) vzorce trojitého uhla

g) univerzálna substitúcia

h) zníženie stupňa

16. cos 2 (3x/7);

Študenti na notebooku pred každým vzorcom vidia svoje odpovede.

Práca je okamžite kontrolovaná počítačom. Výsledky sa zobrazia na veľkej obrazovke pre každého.

Taktiež po skončení práce sa správne odpovede zobrazujú žiakom na notebookoch. Každý žiak vidí, kde sa stala chyba a aké vzorce potrebuje zopakovať.

3. Zjednodušenie goniometrických výrazov. (25 min.)

Cieľom je zopakovať, vypracovať a upevniť aplikáciu základných vzorcov trigonometrie. Riešenie úloh B7 zo skúšky.

V tejto fáze je vhodné rozdeliť triedu na skupiny silných (pracujú samostatne s následným overením) a slabých žiakov, ktorí spolupracujú s učiteľom.

Zadanie pre silných študentov (pripravené vopred na tlačenom základe). Hlavný dôraz sa kladie na vzorce zmenšenia a dvojitého uhla podľa USE 2011.

Zjednodušte výrazy (pre silných študentov):

Paralelne učiteľ pracuje so slabými žiakmi, diskutuje a rieši úlohy na obrazovke pod diktátom žiakov.

Vypočítať:

5) sin (270º - α) + cos (270º + α)

Zjednodušiť:

Na rad prišla diskusia o výsledkoch práce silnej skupiny.

Odpovede sa zobrazia na obrazovke a tiež pomocou videokamery sa zobrazia práce 5 rôznych študentov (pre každého jedna úloha).

Slabá skupina vidí podmienku a spôsob riešenia. Existuje diskusia a analýza. S využitím technických prostriedkov sa to deje rýchlo.

4. Riešenie najjednoduchších goniometrických rovníc. (30 min.)

Cieľom je zopakovať, systematizovať a zovšeobecniť riešenie najjednoduchších goniometrických rovníc so zaznamenaním ich koreňov. Riešenie úlohy B3.

Akákoľvek goniometrická rovnica, bez ohľadu na to, ako ju vyriešime, vedie k najjednoduchšej.

Pri vypracovávaní zadania by študenti mali venovať pozornosť písaniu koreňov rovníc konkrétnych prípadov a všeobecného tvaru a výberu koreňov v poslednej rovnici.

Riešiť rovnice:

Napíšte najmenší kladný koreň odpovede.

5. Samostatná práca (10 min.)

Cieľom je otestovať nadobudnuté zručnosti, identifikovať problémy, chyby a spôsoby ich odstránenia.

Podľa výberu študenta sú ponúkané rôzne práce.

Možnosť pre "3"

1) Nájdite hodnotu výrazu

2) Zjednodušte výraz 1 - sin 2 3α - cos 2 3α

3) Vyriešte rovnicu

Možnosť pre "4"

1) Nájdite hodnotu výrazu

2) Vyriešte rovnicu Napíšte najmenší kladný koreň svojej odpovede.

Možnosť pre "5"

1) Nájdite tgα, ak

2) Nájdite koreň rovnice Napíšte najmenší kladný koreň svojej odpovede.

6. Zhrnutie hodiny (5 min.)

Učiteľ zhŕňa skutočnosť, že hodina zopakovala a upevnila goniometrické vzorce, riešenie najjednoduchších goniometrických rovníc.

Domáca úloha sa zadáva (vopred vytlačená) s náhodnou kontrolou na nasledujúcej hodine.

Riešiť rovnice:

10) Uveďte svoju odpoveď ako najmenší kladný koreň.

lekcia 2

Predmet: 11. ročník (príprava na skúšku)

Metódy riešenia goniometrických rovníc. Výber koreňa. (2 hodiny)

Ciele:

Zovšeobecniť a systematizovať poznatky o riešení goniometrických rovníc rôznych typov.
Podporovať rozvoj matematického myslenia žiakov, schopnosť pozorovať, porovnávať, zovšeobecňovať, klasifikovať.
Povzbudzovať žiakov k prekonávaniu ťažkostí v procese duševnej činnosti, k sebakontrole, introspekcii svojich činností.

Vybavenie na lekciu: KRMu, notebooky pre každého študenta.

Štruktúra lekcie:

Orgmoment
Diskusia d/sa samot. práca z poslednej lekcie
Opakovanie metód riešenia goniometrických rovníc.
Riešenie goniometrických rovníc
Výber koreňov v goniometrických rovniciach.
Samostatná práca.
Zhrnutie lekcie. Domáca úloha.

1. Organizačný moment (2 min.)

Učiteľ pozdraví poslucháčov, oznámi tému hodiny a plán práce.

2. a) Rozbor domácej úlohy (5 min.)

Cieľom je skontrolovať výkon. Jedno dielo pomocou videokamery sa zobrazí na obrazovke, ostatné sa selektívne zbierajú, aby ich učiteľ skontroloval.

b) Analýza samostatnej práce (3 min.)

Cieľom je vyriešiť chyby, naznačiť spôsoby, ako ich prekonať.

Na obrazovke sú odpovede a riešenia, študenti vopred vydali svoje práce. Analýza prebieha rýchlo.

3. Opakovanie metód riešenia goniometrických rovníc (5 min.)

Cieľom je pripomenúť si metódy riešenia goniometrických rovníc.

Opýtajte sa žiakov, aké metódy riešenia goniometrických rovníc poznajú. Zdôraznite, že existujú takzvané základné (často používané) metódy:

variabilná substitúcia,
faktorizácia,
homogénne rovnice,

a tam sú použité metódy:

podľa vzorcov na prepočet sumy na súčin a súčinu na súčet,
podľa redukčných vzorcov,
univerzálna trigonometrická substitúcia
zavedenie pomocného uhla,
násobenie nejakou goniometrickou funkciou.

Treba tiež pripomenúť, že jedna rovnica môže byť vyriešená rôznymi spôsobmi.

4. Riešenie goniometrických rovníc (30 min.)

Cieľom je zovšeobecniť a upevniť vedomosti a zručnosti na túto tému, pripraviť sa na riešenie C1 z USE.

Považujem za účelné riešiť rovnice pre každú metódu spolu so žiakmi.

Žiak nadiktuje riešenie, učiteľ zapíše na tablet, celý postup sa zobrazí na obrazovke. To vám umožní rýchlo a efektívne obnoviť predtým pokrytý materiál vo vašej pamäti.

Riešiť rovnice:

1) zmena premennej 6cos 2 x + 5sinx - 7 = 0

2) faktorizácia 3cos(x/3) + 4cos 2 (x/3) = 0

3) homogénne rovnice sin 2 x + 3cos 2 x - 2sin2x = 0

4) prevod súčtu na súčin cos5x + cos7x = cos(π + 6x)

5) prevod produktu na súčet 2sinx sin2x + cos3x = 0

6) zníženie stupňa sin2x - sin 2 2x + sin 2 3x \u003d 0,5

7) univerzálna trigonometrická substitúcia sinx + 5cosx + 5 = 0.

8) zavedenie pomocného uhla √3sinx + cosx - √2 = 0

9) násobenie nejakou goniometrickou funkciou cosx cos2x cos4x = 1/8.

5. Výber koreňov goniometrických rovníc (20 min.)

Účelom tejto fázy lekcie je preto pripomenúť si predtým preštudovaný materiál, pripraviť sa na riešenie problému C1 z USE v roku 2011.

Takéto rovnice sú považované za rovnice so zvýšenou zložitosťou a vo verzii USE sú v druhej časti, konkrétne C1.

Vyriešte rovnicu:

Zlomok je nula, ak potom pomocou jednotkového kruhu vyberieme korene (pozri obrázok 1)

Obrázok 1.

dostaneme x = π + 2πn, n Z

Odpoveď: π + 2πn, n Z

Na obrazovke je výber koreňov zobrazený v kruhu na farebnom obrázku.

Súčin sa rovná nule, keď sa aspoň jeden z faktorov rovná nule a oblúk zároveň nestráca svoj význam. Potom

Pomocou jednotkového kruhu vyberte korene (pozri obrázok 2)

Obrázok 2

Poďme do systému:

V prvej rovnici systému urobíme zmenu log 2 (sinx) = y, získame rovnicu potom , späť do systému

pomocou jednotkového kruhu vyberieme korene (pozri obrázok 5),

Obrázok 5

6. Samostatná práca (15 min.)

Cieľom je upevniť a skontrolovať asimiláciu materiálu, identifikovať chyby a načrtnúť spôsoby ich opravy.

Práca je ponúkaná v troch verziách, pripravených vopred v tlačenej podobe, podľa výberu študentov.

Rovnice sa dajú riešiť akýmkoľvek spôsobom.

Možnosť pre "3"

Riešiť rovnice:

1) 2 sin 2 x + sinx - 1 = 0

2) sin2x = √3cosx

Možnosť pre "4"

Riešiť rovnice:

1) cos2x = 11sinx - 5

2) (2sinx + √3) log 8 (cosx) = 0

Možnosť pre "5"

Riešiť rovnice:

1) 2sinx - 3cosx = 2

7. Zhrnutie hodiny, domáca úloha (5 min.)

Učiteľ zhrnie lekciu, ešte raz upozorní na skutočnosť, že goniometrickú rovnicu možno riešiť viacerými spôsobmi. Najlepší spôsob, ako dosiahnuť rýchly výsledok, je ten, ktorý sa najlepšie naučí konkrétny študent.

Pri príprave na skúšku je potrebné systematicky opakovať vzorce a metódy riešenia rovníc.

Domáce úlohy (vopred pripravené na tlačenom základe) sú rozdelené a spôsoby riešenia niektorých rovníc sú komentované.

Riešiť rovnice:

1) cosx + cos5x = cos3x + cos7x

2) 5sin(x/6) - cos(x/3) + 3 = 0

3) 4sin 2x + sin2x = 3

4) hriech 2 x + hriech 2 2x - hriech 2 3x - hriech 2 4x = 0

5) cos3x cos6x = cos4x cos7x

6) 4sinx - 6cosx = 1

7) 3sin2x + 4 cos2x = 5

8) cosx cos2x cos4x cos8x = (1/8) cos15x

9) (2sin 2 x - sinx)log 3 (2cos 2 x + cosx) = 0

10) (2cos 2 x - √3cosx) log 7 (-tgx) = 0

11)